Графический метод с использованием характеристик
по первым гармоникам
При анализе нелинейной цепи данным методом изменяющиеся по сложному закону переменные величины заменяются их первыми гармониками , что позволяет использовать векторные диаграммы.
Основные этапы расчета:
- строится график зависимости 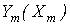 нелинейного элемента для первых гармоник;
нелинейного элемента для первых гармоник;
- произвольно задаются амплитудой одной из переменных , например ![]() , связанной с нелинейным элементом , и по характеристике
, связанной с нелинейным элементом , и по характеристике 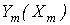 последнего находят другую переменную
последнего находят другую переменную ![]() , определяющую режим работы нелинейного элемента , после чего , принимая все величины синусоидально изменяющимися во времени , на основании построения векторной диаграммы определяется амплитуда первой гармоники
, определяющую режим работы нелинейного элемента , после чего , принимая все величины синусоидально изменяющимися во времени , на основании построения векторной диаграммы определяется амплитуда первой гармоники ![]() переменной на входе цепи;
переменной на входе цепи;
- путем построения ряда векторных диаграмм для различных значений ![]() строится зависимость
строится зависимость 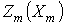 , по которой для заданного значения
, по которой для заданного значения ![]() определяется действительная величина
определяется действительная величина ![]() , на основании чего проводится окончательный анализ цепи.
, на основании чего проводится окончательный анализ цепи.
Графический метод с использованием характеристик
для действующих значений (метод эквивалентных синусоид)
При анализе нелинейной цепи данным методом реальные несинусоидально изменяющиеся переменные заменяются эквивалентными им синусоидальными величинами , действующие значения которых равны действующим значениям исходных несинусоидальных переменных. Кроме того , активная мощность , определяемая с помощью эквивалентных синусоидальных величин , должна быть равна активной мощности в цепи с реальной (несинусоидальной) формой переменных. Используемый прием перехода к синусоидальным величинам определяет другое название метода - метод эквивалентных синусоид.
Строго говоря, характеристика нелинейного элемента для действующих значений зависит от формы переменных , определяющих эту характеристику. Однако в первом приближении , особенно при качественном анализе , этим фактом обычно пренебрегают , считая характеристику неизменной для различных форм переменных. Указанное ограничивает возможности применения метода для цепей , где высшие гармоники играют существенную роль , например, для цепей с резонансными явлениями на высших гармониках.
Переход к эквивалентным синусоидам позволяет использовать при анализе цепей векторные диаграммы. В связи с этим этапы расчета данным методом в общем случае совпадают с рассмотренными в предыдущем разделе.
Метод расчета с использованием характеристик для действующих значений широко применяется для исследования явлений в цепях , содержащих нелинейную катушку индуктивности и линейный конденсатор (феррорезонансных цепях) , или цепях с линейной катушкой индуктивности и нелинейным конденсатором. Кроме того , данный метод применяется для анализа цепей с инерционными нелинейными элементами , у которых постоянная времени , характеризующая их инерционные свойства , много больше периода переменного напряжения (тока) источника питания. В этом случае в установившихся режимах инерционные нелинейные элементы можно рассматривать как линейные с постоянными параметрами (сопротивлением , индуктивностью , емкостью). При этом сами параметры определяются по характеристикам нелинейных элементов для действующих значений и для различных величин последних являются разными.
Феррорезонансные явления
Различают феррорезонанс в последовательной цепи (феррорезонанс напряжений) и феррорезонанс в параллельной цепи (феррорезонанс токов).
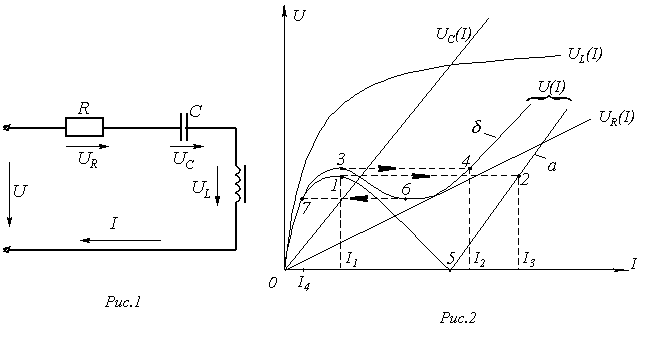
Рассмотрим первый из них на основе схемы на рис. 1. Для этого строим (см. рис. 2) прямую зависимости 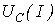 , определяемую соотношением
, определяемую соотношением
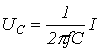 . . |
(1) |
Далее для двух значений сопротивлений 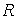 (
( ![]() и
и ![]() ) строим графики зависимостей
) строим графики зависимостей ![]() : для
: для ![]() - согласно соотношению
- согласно соотношению ![]() (кривая
(кривая ![]() на рис. 2); для
на рис. 2); для ![]() - согласно выражению
- согласно выражению 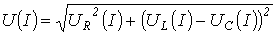 (кривая
(кривая ![]() на рис. 2).
на рис. 2).
Точка пересечения кривой 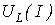 с прямой
с прямой 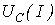 соответствует феррорезонансу напряжений. Феррорезонансом напряжений называется такой режим работы цепи , содержащей последовательно соединенные нелинейную катушку индуктивности и конденсатор , при котором первая гармоника тока в цепи совпадает по фазе с синусоидальным питающим напряжением. В соответствии с данным определением при рассмотрении реальной катушки действительная вольт-амперная характеристика (ВАХ) цепи , даже при значении сопротивления последовательного включаемого резистора
соответствует феррорезонансу напряжений. Феррорезонансом напряжений называется такой режим работы цепи , содержащей последовательно соединенные нелинейную катушку индуктивности и конденсатор , при котором первая гармоника тока в цепи совпадает по фазе с синусоидальным питающим напряжением. В соответствии с данным определением при рассмотрении реальной катушки действительная вольт-амперная характеристика (ВАХ) цепи , даже при значении сопротивления последовательного включаемого резистора ![]() , в отличие от теоретической (кривая
, в отличие от теоретической (кривая ![]() на рис. 2) не касается оси абсцисс и смещается влево , что объясняется наличием высших гармоник тока , а также потерями в сердечнике катушки. С учетом последнего напряжение на катушке индуктивности
на рис. 2) не касается оси абсцисс и смещается влево , что объясняется наличием высших гармоник тока , а также потерями в сердечнике катушки. С учетом последнего напряжение на катушке индуктивности 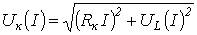 , где
, где ![]() - сопротивление , характеризующее потери в сердечнике , в режиме феррорезонанса
- сопротивление , характеризующее потери в сердечнике , в режиме феррорезонанса 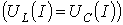 не равно напряжению на конденсаторе.
не равно напряжению на конденсаторе.
Из построенных результирующих ВАХ цепи видно , что при увеличении питающего напряжения в цепи имеет место скачок тока: для кривой ![]() - из точки 1 в точку 2 , для кривой
- из точки 1 в точку 2 , для кривой ![]() - из точки 3 в точку 4. Аналогично имеет место скачок тока при снижении питающего напряжения: для кривой
- из точки 3 в точку 4. Аналогично имеет место скачок тока при снижении питающего напряжения: для кривой ![]() - из точки 5 в точку 0; для кривой
- из точки 5 в точку 0; для кривой ![]() - из точки 6 в точку 7. Явление скачкообразного изменения тока при изменении входного напряжения называется триггерным эффектом в последовательной феррорезонансной цепи.
- из точки 6 в точку 7. Явление скачкообразного изменения тока при изменении входного напряжения называется триггерным эффектом в последовательной феррорезонансной цепи.
В соответствии с уравнением
| (2) |
на рис. 3 и 4 построены векторные диаграммы для двух произвольных значений тока ( 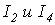 ) в режимах до и после резонанса для обеих ВАХ (для
) в режимах до и после резонанса для обеих ВАХ (для ![]() - соответственно рис. 3 , а и 3 , б; для
- соответственно рис. 3 , а и 3 , б; для ![]() - рис. 4 , а и 4 , б); при этом соответствующие выбранным токам действующие значения напряжений , входящих в (2) , взяты из графиков на рис. 2.
- рис. 4 , а и 4 , б); при этом соответствующие выбранным токам действующие значения напряжений , входящих в (2) , взяты из графиков на рис. 2.
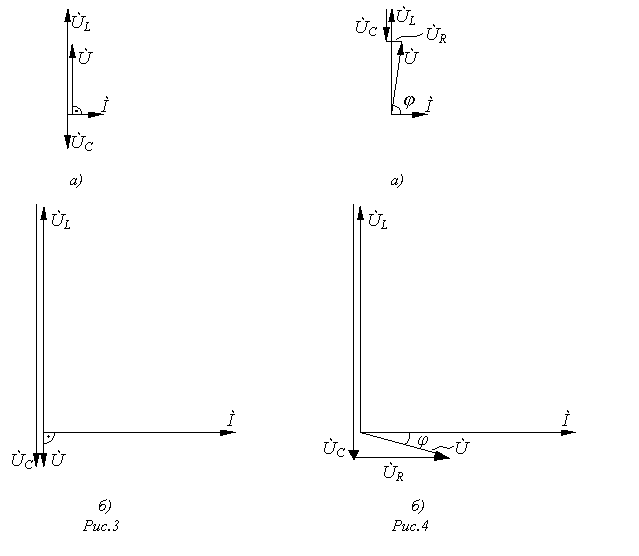
Анализ векторных диаграмм позволяет сделать вывод , что в режиме до скачка тока напряжение на входе цепи опережает по фазе ток , а после скачка - отстает , т.е. в первом случае нагрузка носит индуктивный характер , а во втором - емкостной. Таким образом , скачок тока в феррорезонансной цепи сопровождается эффектом опрокидывания фазы.
Феррорезонанс в параллельной цепи рассмотрим на основе схемы на рис. 5. Для этого, как и в предыдущем случае, строим (см. рис. 6) прямую 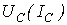 , определяемую выражением (1).
, определяемую выражением (1).
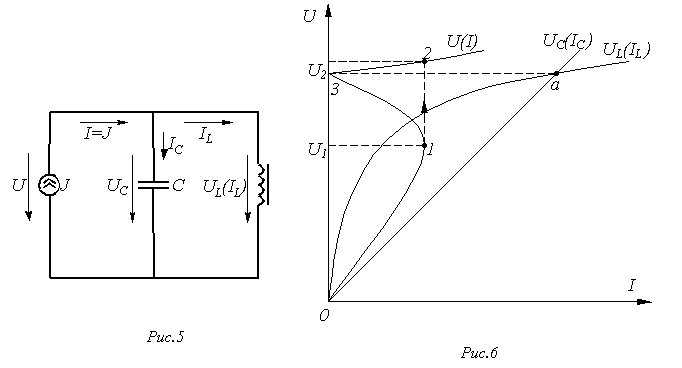
Далее, поскольку ![]() , в соответствии с соотношением
, в соответствии с соотношением ![]() строим результирующую ВАХ
строим результирующую ВАХ ![]() цепи.
цепи.
Точка ![]() пересечения кривой
пересечения кривой 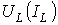 с прямой
с прямой 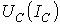 соответствует феррорезонансу токов. Необходимо отметить , что в реальном случае действительная ВАХ цепи в отличие от теоретической не касается оси ординат , что объясняется наличием высших гармоник тока и неидеальностью катушки индуктивности.
соответствует феррорезонансу токов. Необходимо отметить , что в реальном случае действительная ВАХ цепи в отличие от теоретической не касается оси ординат , что объясняется наличием высших гармоник тока и неидеальностью катушки индуктивности.
Из построенной ВАХ ![]() видно , что при увеличении тока источника имеет место скачок напряжения. Явление скачкообразного изменения напряжения при изменении входного тока называется триггерным эффектом в параллельной феррорезонансной цепи.
видно , что при увеличении тока источника имеет место скачок напряжения. Явление скачкообразного изменения напряжения при изменении входного тока называется триггерным эффектом в параллельной феррорезонансной цепи.
На рис. 7 для двух (до и после резонанса) значений напряжения ( ![]() и
и ![]() ) построены векторные диаграммы; при этом соответствующие выбранным напряжениям действующие значения токов
) построены векторные диаграммы; при этом соответствующие выбранным напряжениям действующие значения токов ![]() и
и ![]() взяты из графиков на рис. 6.
взяты из графиков на рис. 6.
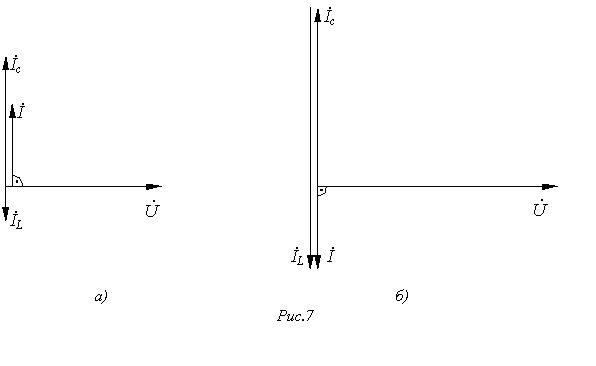
Анализ векторных диаграмм показывает , что в режиме до скачка напряжения ток источника опережает по фазе входное напряжение (рис. 7,а) , а после скачка (рис. 7,б) - отстает , т.е. в первом случае нагрузка носит емкостной характер , а во втором - индуктивный. Таким образом , скачок напряжения связан с эффектом опрокидывания фазы.
Аналитические методы расчета
Аналитические методы , в отличие от рассмотренных выше графических , позволяют проводить анализ нелинейной цепи в общем виде , а не для частных значений параметров элементов схемы. В этом заключается их главное преимущество. Однако аппроксимация нелинейной характеристики , лежащая в основе данных методов , изначально обусловливает внесение в расчеты большей или меньшей погрешности. Как и при графическом анализе цепей , при применении аналитических методов используются характеристики нелинейных элементов для мгновенных значений , по первым гармоникам и для действующих значений. При этом для расчета цепей переменного тока наиболее широкое распространение получили следующие аналитические методы:
В первых трех случаях обычно используются характеристики нелинейных элементов для мгновенных значений. Характеристики нелинейных элементов по первым гармоникам используются при применении частного варианта метода гармонического баланса - метода расчета по первым гармоникам. В свою очередь , метод эквивалентных синусоид основан на применении характеристик нелинейных элементов для действующих значений.
Метод аналитической аппроксимации
Данный метод основан на аппроксимации характеристик нелинейных элементов аналитическими выражениями с последующим аналитическим решением системы нелинейных уравнений состояния цепи. Точность , а с другой стороны , сложность расчета методом аналитической аппроксимации непосредственно зависят от вида принятой аналитической функции , аппроксимирующей характеристику нелинейного элемента. Поэтому ее выбор является важнейшим этапом при анализе цепи данным методом. Как уже отмечалось , для получения большей точности расчета необходимо выбирать аппроксимирующую функцию , наиболее полно соответствующую исходной нелинейной характеристике , что , однако , может привести в общем случае к появлению в уравнениях состояния сложных математических выражений , часто трудно разрешимых (или вообще неразрешимых) аналитически. С другой стороны , принятие чрезмерно простой функции для аппроксимации позволяет достаточно быстро получить результат , однако погрешность расчета может оказаться недопустимо высокой. Таким образом , выбор аппроксимирующей функции во многом зависит от поставленной задачи расчета и требуемой точности его результатов.
Пусть, например, в цепи состоящей из последовательно соединенных источника тока с 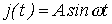 и нелинейной катушки индуктивности, заданная графически вебер-амперная характеристика которой может быть аппроксимирована выражением
и нелинейной катушки индуктивности, заданная графически вебер-амперная характеристика которой может быть аппроксимирована выражением
| (3) |
требуется найти напряжение на индуктивном элементе.
На первом этапе определяем коэффициенты 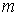 и
и ![]() аппроксимирующей функции с учетом того, что рабочий участок заданной графически кривой
аппроксимирующей функции с учетом того, что рабочий участок заданной графически кривой ![]() ограничен сверху амплитудой А тока в цепи, что сразу дает одну из двух точек аппроксимации.
ограничен сверху амплитудой А тока в цепи, что сразу дает одну из двух точек аппроксимации.
После этого подставляем в (3) выражение 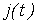 , в результате чего получаем
, в результате чего получаем
![]()
или, с учетом соотношения
![]()
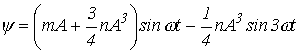 .
.
Тогда искомое напряжение на катушке индуктивности
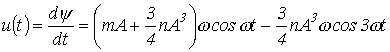 .
.
Литература
Контрольные вопросы и задачи
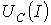 , обеспечивающую скачок тока с увеличением напряжения при заданной величине
, обеспечивающую скачок тока с увеличением напряжения при заданной величине 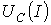 , обеспечивающую триггерный эффект при заданной величине
, обеспечивающую триггерный эффект при заданной величине